A tree is a combination of a finite set of elements, called nodes and a finite set of directed lines, called branches that connect the nodes.
The number of branches associated with a node is the degree of the node. When the branch is directed towards the node, it is an indegree branch. When the branch is directed away from the node, it is an out degree branch, the sum of outdegree and indegree branches equal to the degree of the node.
Some important terms:
- Root node: If the tree is non empty, then the first node is called as root. The indegree of root by definition is zero.
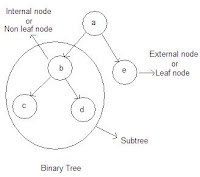
- Leaf node: A node with no successors (nodes after it). There will usually be many leaves in a tree.
- Non Leaf node: A node which has both a parent and at least one child.
- Internal nodes: Nodes that are not root and not leaf are called as internal nodes
- Parent node: A node is a parent if it has successor nodes; means out degree greater than zero.
- Child node: A node is child node if indegree is one.
- Siblings: Two or more nodes with same parent are siblings.
- Ancestor node: An ancestor is any node in the path from the root to the node.
- Descendant node: A descendent is any node on the path below the parent node.
- Subtree: A subtree is any connected structure below the root.
- Directed tree: A directed tree is an acyclic digraph, which has only one node with indegree 0, and others nodes have indegree 1.
- Binary tree: A binary tree is a tree in which no node can have more than two subtrees. In other word it is a directed tree in which outdegree of each node is less than or equal to two. (i.e. zero, one or two). An empty tree is also a binary tree.
- Strictly binary tree: If the outdegree of every node in a tree is either 0 or 2, then the tree is said to be strictly binary tree. i.e. each node can have maximum two children or empty left and empty right child.
- Complete binary tree: A strictly binary tree in which the number of nodes at any level i is 2 i-1 then the tree is said to be complete binary tree.
- Almost binary tree: A tree of depth d is an almost complete binary tree, if the tree is complete up to the level d-1.
- Tree traversals: Tree traversal is the technique in which each node in the tree is processed or visited exactly once systematically one after the other. The different tree traversal techniques are Inorder, Preorder and Postorder.Algorithm for tree traversal
- Traverse the left sub tree in inorder [L]
- Process the root node [N]
- Traverse the right sub tree in inorder [R]
- Process the root node [N]
- Traverse the left sub tree in preorder [L]
- Traverse the right sub tree in Preorder [R]
- Traverse the left subtree in post order. [L]
- Traverse the Right sub tree in postorder [R]
- Process the root node [N]
Binary Search tree: A binary search tree is a binary tree in which for each node say x in the tree elements in the left subtree are less than info(x) and elements in the left subtree are greater or equal to info(x).
The operations performed on binary search tree are:
- Insertion: An item is inserted
- Searching: Search for a specific item in the tree.
- Deletion: Deleting a node from a given tree.
Balanced Search trees: Balanced search tree is on that exhibits a good ratio of breadth to depth. There are special classes of Balanced Search Trees that are self-balancing. That is as new nodes are added or existing nodes are deleted, these Balanced search Trees automatically adjust their topology to maintain an optimal balance. With an ideal balance, the running time for inserts, searches, and deletes even in the worst case is log2n.
AVL Trees: An AVL tree is a binary search tree whose left subtree and right subtree differ in height by at most 1 unit, and whose left and right trees are also AVL trees.
To maintain balance in a height balanced binary tree, each node will have to keep an additional piece of information that is needed to efficiently maintain balance in the tree after every insert and delete operation has been performed. For an AVL tree, this additional piece of information is called the balance factor and it indicates if the difference in height between the left and right subtrees is the same or, if not, which of the two subtrees has height one unit larger. If a node has a balance factor rh(right high). It indicates that the height of the left subtree. Similarly the balance factor for a node could be lh(left height) or eh(equal height).
Binary Heap tree: A binary heap is a complete binary tree. A tree that is completely filled except possibly at the bottom level, which is filled from left to right with no missing nodes.
You Might also view the following Related Posts
- Fundamental of data structures
- Definition of Stack
- Definition of Queues
- Definition of List and Linked List
- Graph Definition

إرسال تعليق